3 線形微分方程式とラプラス変換と伝達関数 31 線形性と時不変性 311 線形性 未知数に定数をかけたものの和だけからなる方程式を線形方程式(lienarequation)と呼び,そ うでないものを非線形方程式(nonlinearequation)と呼びます。たとえば,x,y,zを未知数と 微分の定義と関数方程式 (19年 東工大) 今回は19年の東工大入試から関数方程式をピックアップします。 上記のようなタイプの問題は出題頻度こそ高くありませんが、いざ出題された場合に類題経験の有無が非常に大きな差となります。 本問のような判別式 :2次方程式の解の個数を判定するための式 特定の範囲に解が存在するための条件 問題演習 指数関数 対数関数 三角関数 いろいろな関数 y = 1 x;

京都大学 関数方程式 受験数学 Youtube
関数 方程式 恒等式
関数 方程式 恒等式-方程式を解く 関数電卓では、solve機能を使うことで、x 23x2=0などの方程式を解くことができます。 solve機能を使うためには、数式を入力した後に、 キー、 キーの順にキーを押します。 正の数と負の数 22 文字と式(中学) 19 一次方程式 23 比例と反比例(中学) 16 平面図形(中学) 33 高校数学全般 6 実数 32 展開と因数分解 28 集合と命題 38 一次不等式 18 二次関数 101 三角比 77 データの分析 45 場合の数 53 確率 75 整数 平面図形 26 空間図形 9




東北大数学ー関数方程式ー 虚空が数学をやるブログ
両辺を u(x,t) = X(x)T(t) で割る 左辺は x のみの関数,右辺は t のみの関数なので, どんな x, t に対してもこの式が成り立つためには,両辺が x にも t にも無関係の定数 に等しくなければならない 方程式。関数。 どちらも中学生になってから学ぶ範囲です。 そして、世の中学生、高校生たちを「数学嫌い」に陥らせる一番の原因でもあります。 まず数学が嫌いになる子は「文字式」の扱いから頭がこんがらがってしまい、考えることを終了してしまうのですが、そんな手痛い洗礼を 数と式(方程式と不等式) 2次関数(グラフと最大・最小) 2次関数(2次方程式と2次不等式) 集合・命題・条件・論理・証明;
隠れているというか、その方程式の解がどこなのかが視覚的に見えます。 それは上の方程式は関数 \(y=2x3\) の \(y\) を \(0\) にしたものであるから、グラフでいうと直線の \(x\) 軸との交点の \(x\) 座標です。 わかりましたか?★ 方程式と関数 例えば 3 日本大百科全書(ニッポニカ) 関数方程式の用語解説 関数を未知の要素とする方程式。微分方程式、積分方程式、微積分方程式、差分方程式、その他いろいろある。たとえば、すべての実数値x、yについて f(x+y)=f(x)+f(y)も関数方程式である。これは、コーシーの方程式といい、fが連続なら解
1 微分方程式とは何か? 未知関数とその導関数を含む方程式を微分方程式(differential equation) という1。 微分方程式は微分積分学とほぼ同じくらいの長い歴史を持つ2。当初は主に物理学由来の問題(有 関数方程式とは,\ 文字通り関数についての方程式(関係式)である 次の型が頻出である\ 結果を覚えておくと問題の見通しが良くなる f(xy)=f(x)f(y)} & → f(x)=ax} f(xy)=f(x)f(y)2xy} & → f(x)=x²ax} f(xy)=f(x)f(y)} & → f(x)=alog x} f(xy)=f(x)f(y)} & → f(x)=e^{ax 関数方程式は,\ 連続や微分可能の条件を付加すること偏微分方程式入門 13年度微分方程式2 講義ノート 桂田祐史 katurada AT meijiacjp http//nalabmindmeijiacjp/~mk/pde/ 13年9月, 21年1




関数方程式の問題再び 聖マリアンナ医科大学医学部の入試問題 身勝手な主張




なぜtとおいて計算しなければならないのですか Clear
式が形式的にこのような形の微分方程式 \p(x,\ y)\,dx q(x,\ y)\,dy = 0 \tag{1}\ を 全微分型微分方程式 といい,その中で,特に2つの式 \(p(x,\ y)\) と \(q(x,\ y)\) とが,それぞれ,ある関数の \(x\) 偏導関数と \(y\) 偏導関数になっているとき,微分方程式 \((1)\) を 完全 方程式と関数の違いって何ですか? 方程式は,小学校の時にやった, +2=3。 を求めましょうのように,分からないところを求めるために使う式のことを言います。一方,関数というのは,「数の関係」です。かならず,2つの数の関係があります。一方の数字にちょっと計算をさせる 関数方程式 17年12月7日 17年12月21日 関数方程式の問題です。 1. (東京電機大) は で定義された関数で, で微分可能で かつ任意の に対して を満足するものとする.このとき, (1) の値を求めよ.これを利用することにより, を で表せ. (2) を と で
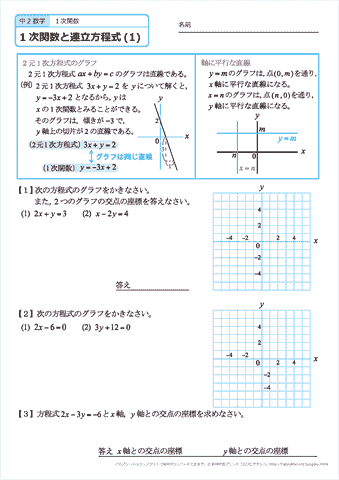



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




方程式と関数の値段と価格推移は 52件の売買情報を集計した方程式と関数の価格や価値の推移データを公開
二次方程式の解の公式と判別式を塾で習ったので三次以上である高次方程式も解の公式や判別式があルのではないかとおもったから ご意見・ご感想 三乗根(立方根)によって解くのでぐっとレベルが高くなったと思った 1310接線の方程式 解説 接線の方程式は,いままでに習った2つの公式の組合わせでできます。 点 (a,b) を通り,傾き m の直線の方程式は y−b = m(x−a) ・・・ (1) (数I) y= f(x) の x = a における接線の傾きは m = f'(a) ・・・(2) (数II) 関数 y= f(x) 上の点 ( a, f(a) ) における接線の方程式はX 2 という式を考えて見ます。 気持ちを切り替えて、 こうした式も 数の「仕組み」の表現 であると考えたのでした。 ただ、「仕組み」の一部に 数字で表せない 部分がある時には、 x という文字を使うのでした。 この x にいろいろな値を 代入して みると




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく
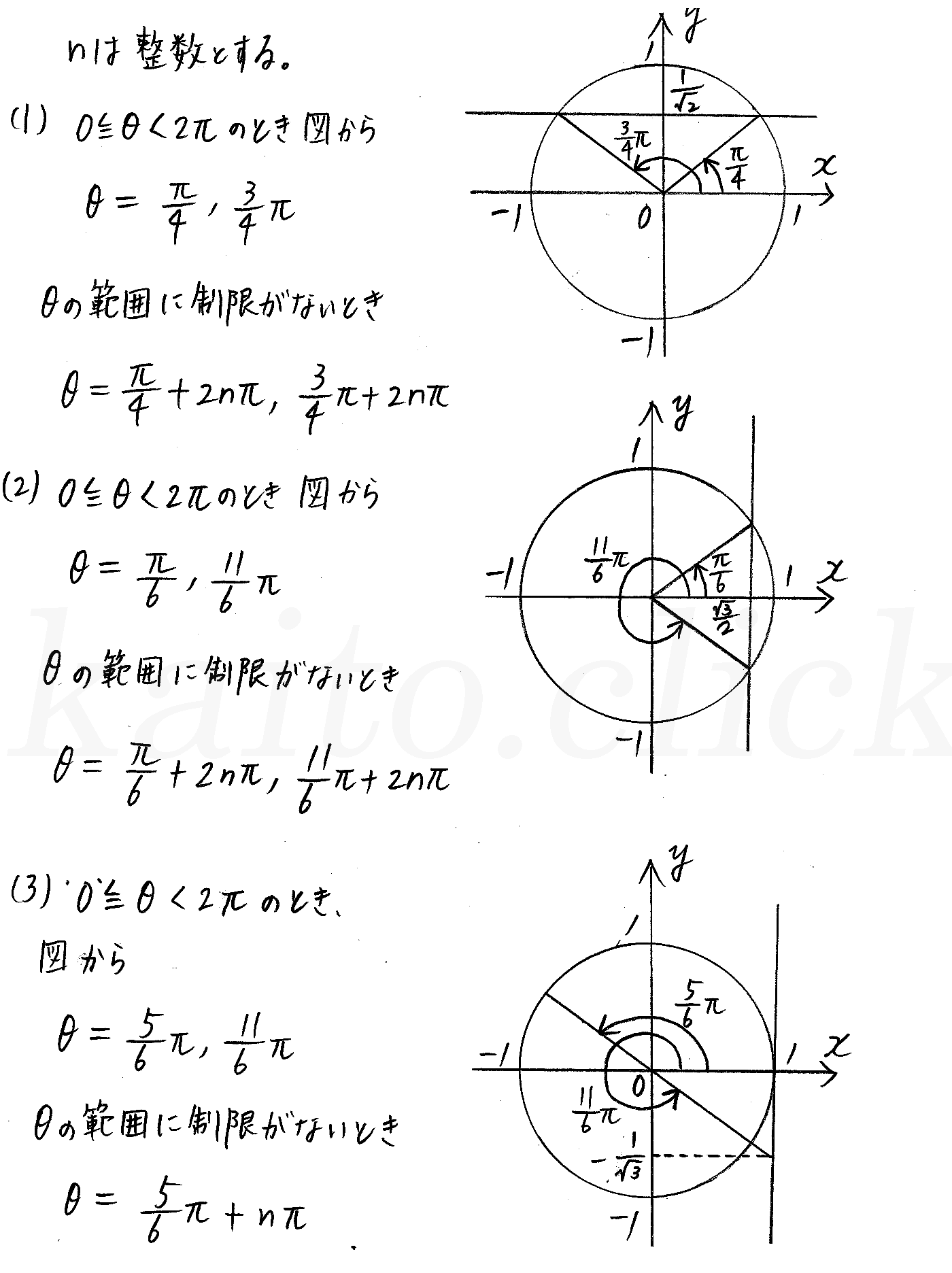



クリアー数学 数2 P58 25 三角関数を含む方程式 不等式
62 第8章関数方程式 1 10 x の関数y(x)の導関数y (x) がxによらず次式を満たすとき, 以下の問に答えよ 2 12x2 2x 2 2x2 1 xx2 xx y x 2 x2 x 1 =0 (1) y = 2x2 1x2 であることを示せ (2) y を求めよ T −57 1 11 x = −kxと初期条件x(0) = 2がある J(k)= ∞ 0 (1k2)xdtで, J(k)を最小にするには, k をいくらにした 微分方程式について 次のような微分方程式があります d^2 x/dx^2 (dy/dx)(4x)/x y*(62x)/x^2 =0 問題は以下です y=ux^2(uはxの関数)がこの微分方程式の解となるために uの満たすべき微分方程式を求めなさい。1 Cauchy functional equation 多くの関数方程式がコーシーの関数方程式(Cauchy functional equation) f(x y) = f(x) f(y) に帰着される. 11 Q における解 f R!




関数方程式f X Y F X F Y 型の解法とコツ 大学受験レベル




数オリ 関数方程式 国際数学オリンピック 17年 第2問 Youtube
陰関数表示とは 右図1の直線の方程式は _____ y= x−1 (1) のように y について解かれた形で表されることが多いが, _____ x−2y−2=0 (2) のように x , y の関係式として表されることもある. (1)のように, _____ y=f(x) の形で, y について解かれた形の関数を陽関数といい,(2)のようにR がコーシーの関数方程式(Cauchy functional equation) f(x y) = f(x) f(y) ⃝1 を満たすものとする. 関数の周りにある「方程式」 例えば、 x = 2 のとき、関数 f (x) が y = 4 という値を取る場合は f (2) = 4 と書きます。 これはただ単に、 ある値を関数に代入したときの式 であり、「 x = 2 という値を代入したときに 4 という値が返される」という事実を説明しているだけの式です。 因みに、関数の文字として f がよく使われますが、これは "function" の頭文字から採られているもので




高校数学 三角方程式 不等式 三角関数の合成 受験の月




ラプラス変換 D関数 D関数を含む2階微分方程式 ばたぱら
研究における実験教科書(『関数と方程式i』,『関数 と方程式Ⅱ』,『関数と方程式Ⅲ』)は,従って「意図 したカリキュラム」を顕在化するものであると位置づ けることができる。(溝口,13) 一方,そうした(実験)教科書は,次に「実施した関数方程式研究室 bv 前島正寿 指導教員:竹内慎吾教授 1 はじめに 一般に微分方程式の解を求めることは難しい そこで関数 解析学の観点から微分方程式を見つめなおすことによって, 微分方程式の解の存在と一意性を考察する 本研究では, 関九州関数方程式セミナー 第38回九州における偏微分方程式研究集会 (21年1月25日1月26日) 研究集会「非線型の諸問題」 (第16回:年9月8日9月9日) 研究集会「若手のための偏微分方程式と数学解析」 (第14回:21年2月18日2月19日)




一次関数 式の求め方をパターン別に問題解説 数スタ




ダランベール方程式のグリーン関数を導出 物理 プログラミング日記
が得られます。C,D は任意定数です。 こうして任意定数を2つ含む解が得られました。 次にa < 0の場合を考えます。はじめの例に挙げた指数関数ex は,何回微分しても元もまま ですから y′′ = y もみたします。これはa = −1のときの微分方程式(16)ですね。そこで一般のa < 0について関数のグラフについて接線の傾きは微分係数に等しいことが分かっていますから,上の式を用いて接線の方程式を求めることができます。 例題1 放物線 \(y = x^2 2x\ \cdots\ (*)\) は,原点を通る曲線です。原点における放物線 \((*)\) の接線の方程式を求め 数学 および 物理学 では、 熱方程式 は特定の 偏微分方程式 。熱方程式の解は、 カロリー関数 として知られることもあります。熱方程式の理論は、 熱 などの量が特定の領域をどのように拡散するかをモデル化する目的で、12年に ジョゼフフーリエ によって最初に開発されました。




高校数学 数 勉強動画 対数関数 方程式編の問題 19ch




関数方程式を考える1 加法的な関数 身勝手な主張




数学ベクトルの数式 プロット 関数 方程式および代数的 幾何学的な数字は グリッドお手本用紙に手書き でシームレスなテクスチャ のイラスト素材 ベクタ Image




多項式と方程式と関数 算数 数学を10倍楽しく学習させる方法




2次方程式と2次関数 数学i フリー教材開発コミュニティ Ftext




接線の方程式の求め方 数学 苦手解決q A 進研ゼミ高校講座




授業で円の方程式 原点中心 半径1 が関数だと先生が言ってたのですが 円の方程式は1つの独立変数に対して2つの従 Peing 質問箱




信州大学入試問題 関数方程式 微分法 数学 Math Path マスぱす




公文 くもん 算数 数学 教材 プリント I 平方根 2次方程式 不等式 1次関数 2次関数 記入済 中学3年生 高校受験 中学校 売買されたオークション情報 Yahooの商品情報をアーカイブ公開 オークファン Aucfan Com




Paypayフリマ 手書きラミネート下敷き B 中学の関数 方程式のまとめ




京都大学 関数方程式 受験数学 Youtube




関数方程式 基本の4パターン 数学の偏差値を上げて合格を目指す



Q Tbn And9gctngx R5ryhmgbstw4ldeatbfnjegwihz1qb6seir0cxtm68rhk Usqp Cau




関数方程式 早稲田教育17数学第1問 受験で実力を得点に変えよう 家庭教師の心がけ



関数方程式研究室 芝浦工業大学




Amazon 方程式と図形トランプ 関数 図形 微分をカードゲームで遊びながら学べるサイエンストランプ カードゲーム トランプ おもちゃ




2次関数 2次方程式の解の存在範囲と判別式 数学 定期テスト対策サイト



基本計算 三角関数 連立方程式 うしブログ



48s96ub7b0z5f Net Taisuu Houteishiki




非線型関数積分方程式の解の存在定理とその応用 関数方程式の定性的理論とその現象解析への応用




東北大数学ー関数方程式ー 虚空が数学をやるブログ




1研究中 C 数学6 関数f x と関数yとx 等式 不等式 恒等式 方程式 関数 次数次式 元
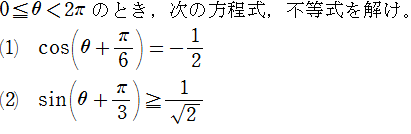



三角関数を含む方程式や不等式 の指導法 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 整式の導関数の関数方程式 受験の月
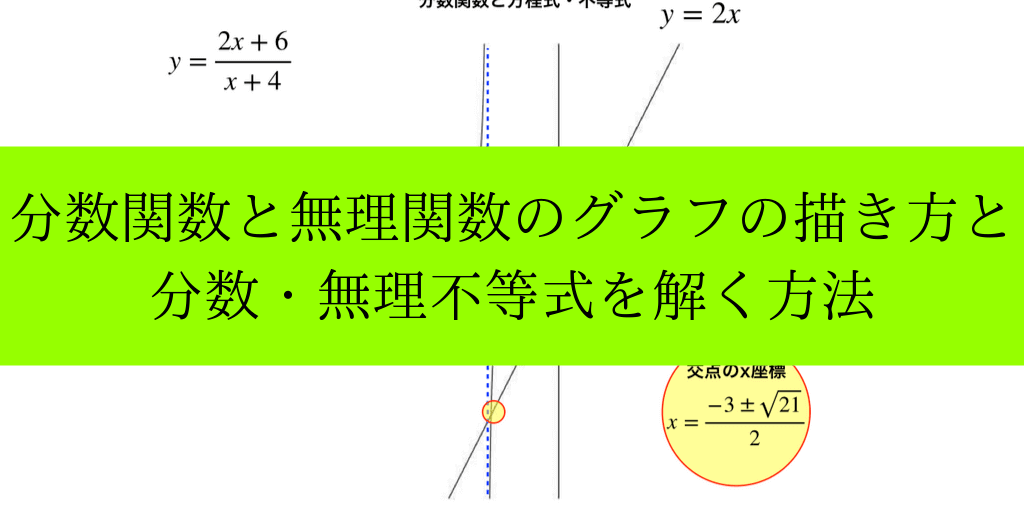



分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法
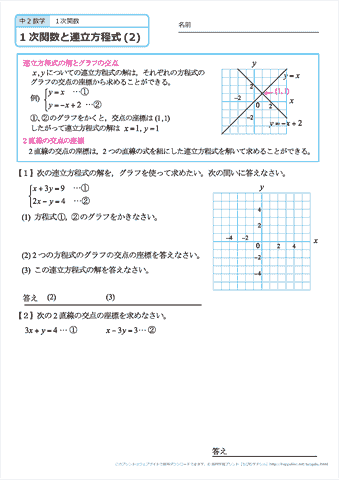



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




全 卓樹 Takuju Zen 道具箱 Researchmap




指数方程式 不等式 指数関数 数学の部屋




リカレント教育 前編 三角関数不要論と個性の壊し方 世界を 数字 で回してみよう 59 働き方改革 18 1 8 ページ Ee Times Japan




書記が数学やるだけ 96 ガウスの微分方程式 ルジャンドルの微分方程式 超幾何関数 鈴華書記 Note




積分で表された関数方程式の問題です F1 数学 箱根駅伝ブログ



3




高校数学 指数方程式 2 例題編 映像授業のtry It トライイット




関数方程式を考える2 いろいろな関数方程式 身勝手な主張




高校数学 関数方程式頻出4パターン 受験の月
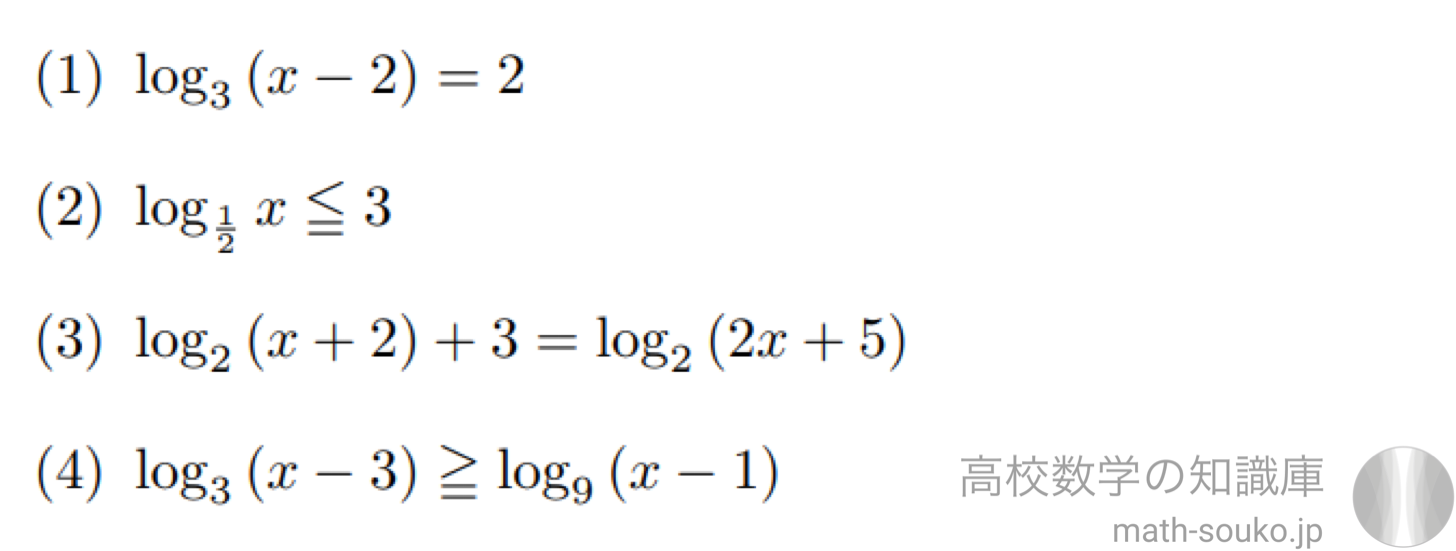



対数方程式と対数不等式の解き方 高校数学の知識庫




プロット 関数方程式と数学のシームレスなパターン のイラスト素材 ベクタ Image




18 318 午前中 最後の講演 日本数学会 東大駒場 関数方程式論分科会 講演書画カメラ用 原稿 12 The Japanese Mathematical Society Annual Meeting At The University Of Tokyo 18 3 18 除算 原稿



関数方程式 微分方程式 京極一樹の数学塾




関数の定義と方程式の変形規則を復習 方程式を解くとは何か ラディカル高校数学



2



関数方程式 微分方程式 京極一樹の数学塾



Kj4



数学iii 第3章 1分数関数 無理関数 逆関数と合成関数 5 無理方程式 無理不等式 Pukiwiki




5講 三角関数を含む方程式 不等式 1節 三角関数 問題集 4章 三角関数 中学生 小学生 高校生のテストや受験対策に おすすめ無料学習問題集 教材サイト




関数方程式




2次関数 2次方程式の解法について 日々是鍛錬 ひびこれたんれん




関数方程式のあやしい世界 Speaker Deck




おもしろいほどよくわかる高校数学 関数編 2次方程式 指数 対数 三角関数がスラスラ解ける サイエンス アイ新書 宮本 次郎 数学 Kindleストア Amazon




1 1 関数と方程式の違い Youtube
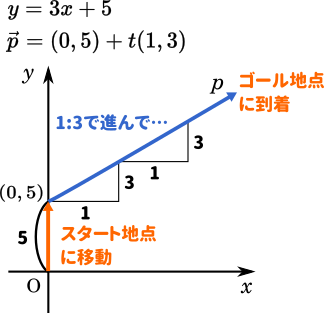



ベクトル方程式と媒介変数表示の仕組み やってることは一次関数と同じ Mm参考書




数学 Ii V Twitter 第1節 三角関数 三角関数を含む方程式 不等式 A 三角関数を含む方程式 例題 0 8 2pのとき 方程式2cos 8 5sin 8 4 0を解け



関数方程式 微分方程式 京極一樹の数学塾




方程式と関数は一緒のもの 数学に関する与太話 ヨタバナ 東大生が語る 勉強になる与太話 Note



タロウ岩井の数学と英語 Noteの補足など 2次方程式や2次関数の平方完成のやり方 Powered By Line
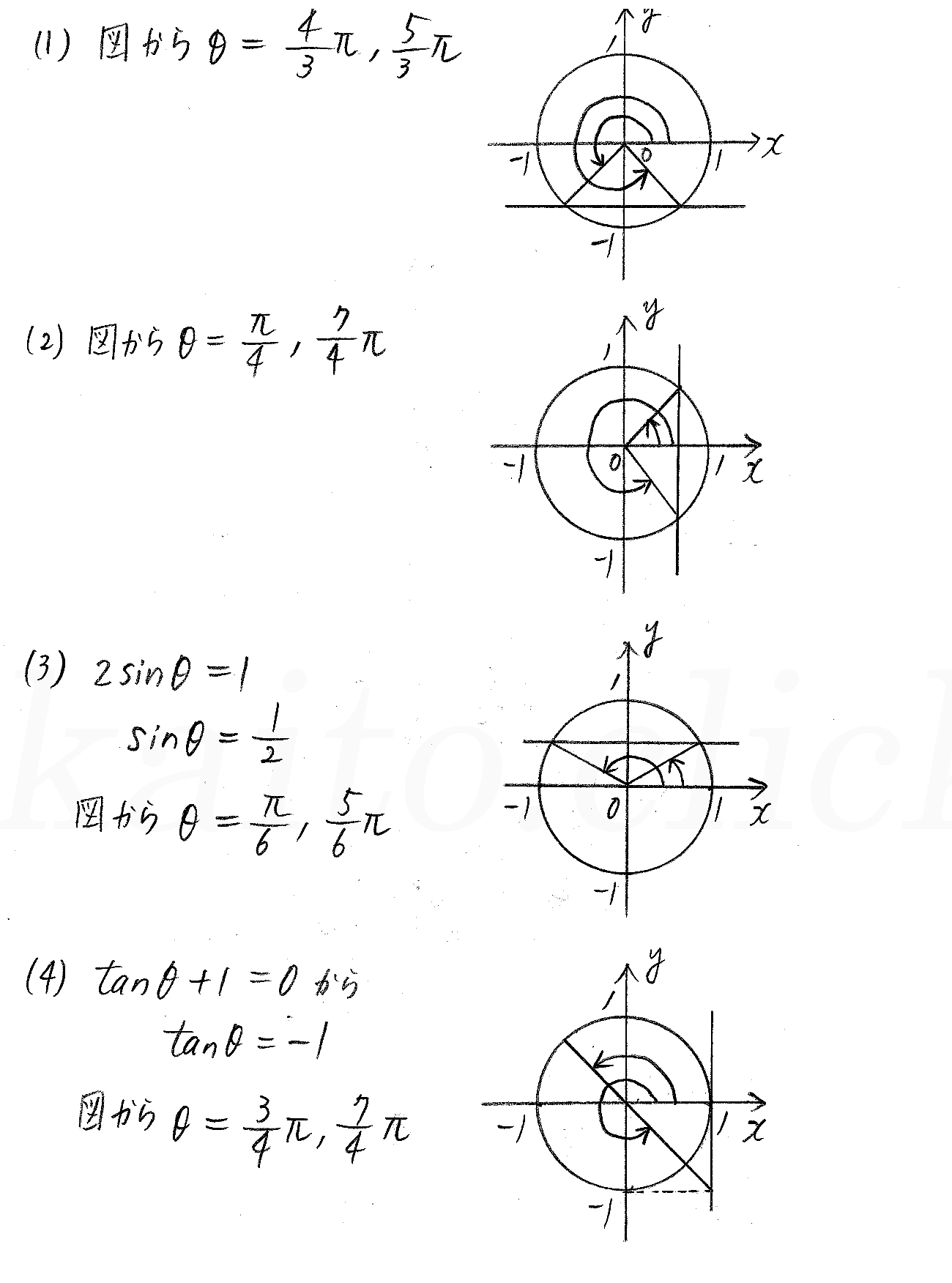



改訂版 3trial数学 P65 5 三角関数を含む方程式 不等式




高校数学 数 勉強動画 三角関数を含む方程式 不等式 の問題 19ch




数学 B 三角関数を解とする2次方程式 立命館大 駒澤大 北里大 大学入試数学の考え方と解法




数学 B 三角関数を含む方程式の解の個数 福岡大 東洋大 国士舘大 大学入試数学の考え方と解法




三角関数を含む方程式の範囲です 赤線以下の問題の解き方がわかりません Clear



株式会社電気書院 D Book 二次関数と二次方程式




一次関数 連立方程式とグラフの関係 苦手な数学を簡単に




関数電卓で連立方程式を解く 某物理教師私有地




ベッセル関数の導出 ベッセル方程式の解法 のんびり固体物理学



高校数学の関数方程式についての質問です 画像の上方に問題分 Yahoo 知恵袋



1




数オリ 関数方程式 19年 国際数学オリンピック Imo Youtube




一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download




関数方程式 Wikipedia
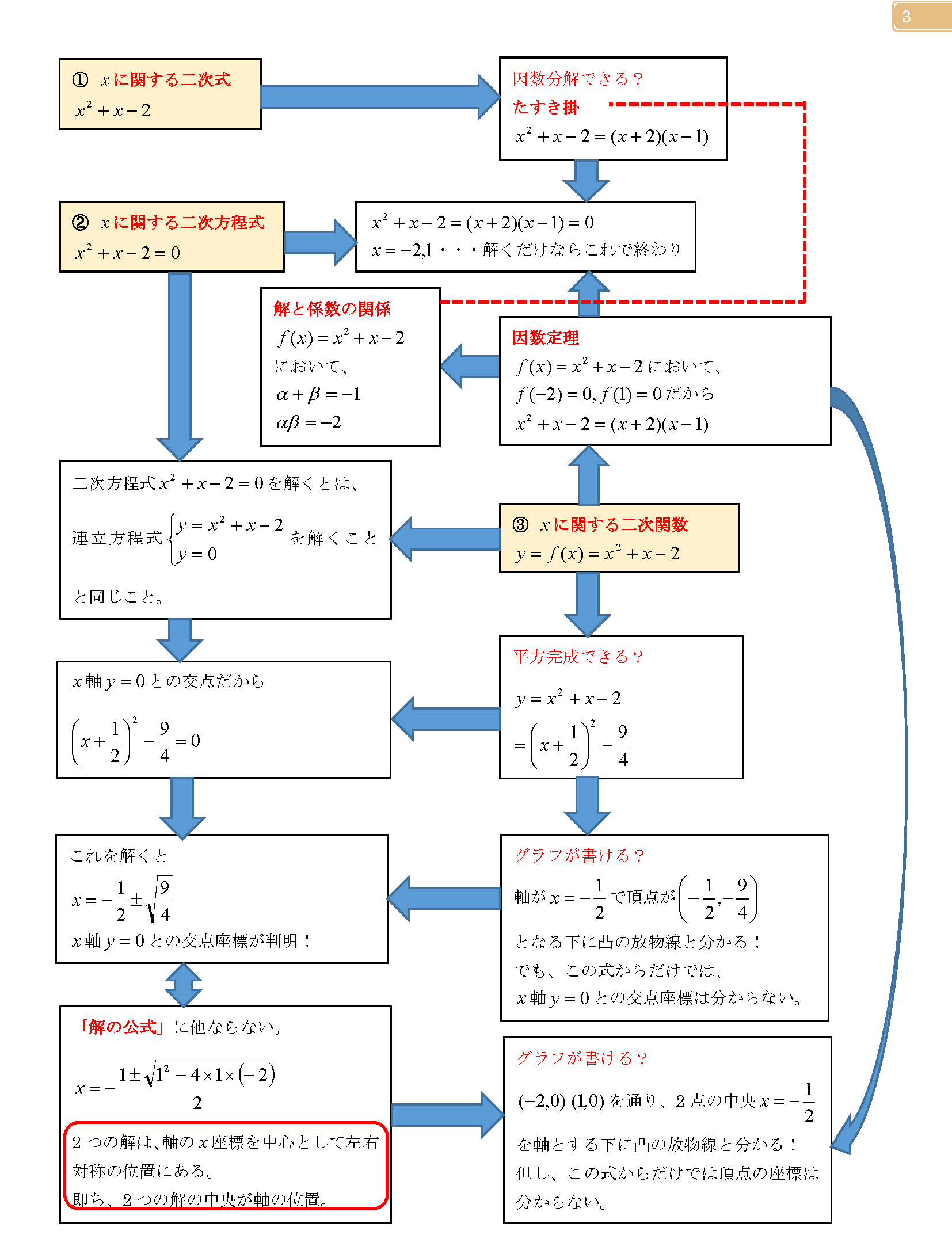



二次式 二次方程式 二次関数が分からん 数学を苦手にさせたのは誰 夏期講座超初級1 勉強法のバイブル 帝都大学へのビジョン



連立方程式と一次関数 名古屋市北区の学習塾は思考力を育む 泰成スクール




どちゃ楽数学bot Twitterren 解答です 入試の関数方程式 ではほぼ微分可能性が与えられています 大抵はf 0 をまず求めさせている気がします 一方で数オリの関数方程式を解くには全射性や単射性など 独特なテクを知る必要があります でも解けると楽しいです 良かっ




関数が決まってしまう 鉄緑会数学講師のひとりごと
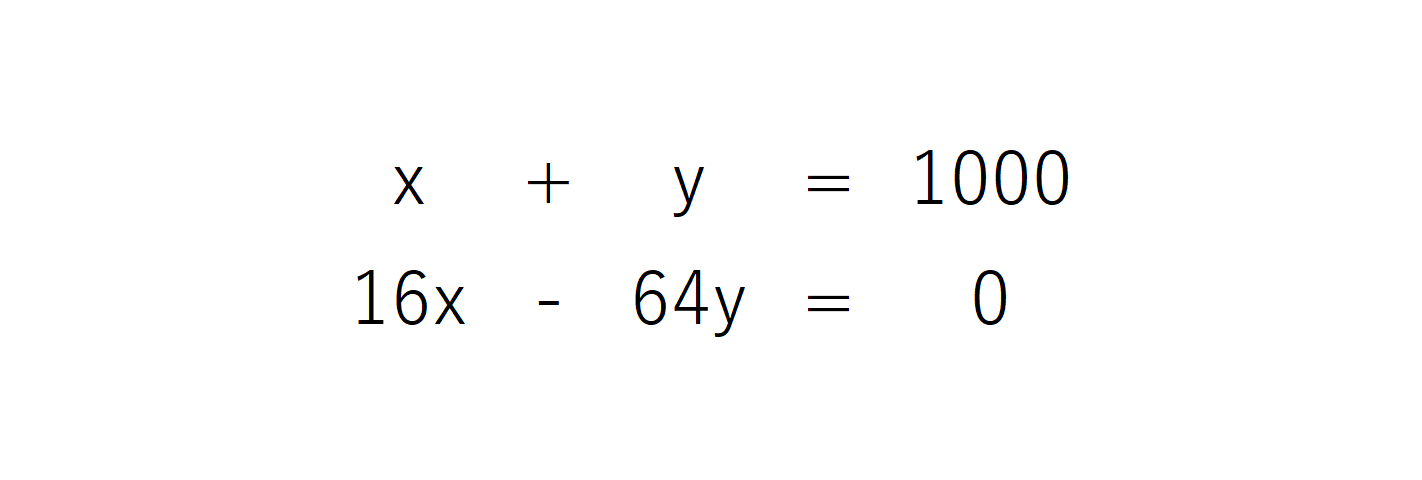



Excel関数 連立方程式 1次方程式 を解く方法 ふみの会社経営日記



Fdkyb3b9c093sr81e Com E8 A3 E6 9e 90 E5 Ad A6 E6 8e A5 E5 B9 E9 9d 86 E5 B1 95 E9 96 8b E9 80 86 E9 96 E6 95 B0 E5 Be Ae E5 86 E6 96 B9 E7 A8 8b E5 8f E9 87 8d



関数方程式 微分方程式 京極一樹の数学塾




2次関数のグラフと方程式




方程式と関数の違いを理解しよう 理系のための備忘録




微分の定義と関数方程式 19年 東工大 数学日和
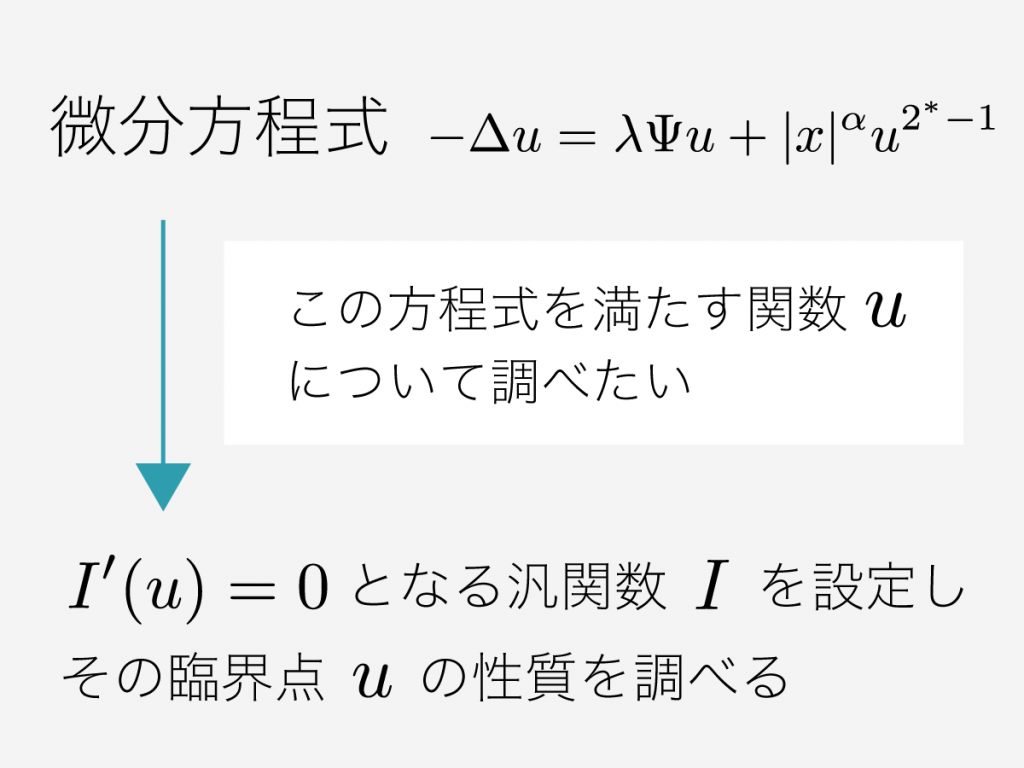



変分法 無限次元空間の臨界点を見出す Laborify




4aswxwfjyeayxm



最も簡単な微分方程式5つ 理数系無料オンライン学習 Kori




三角関数を含む方程式 不等式 の勉強法のわからないを5分で解決 映像授業のtry It トライイット
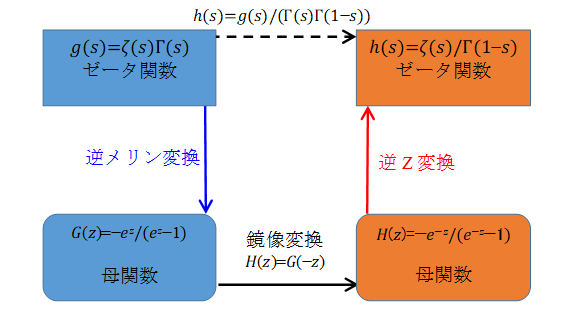



複素解析によるゼータ関数の反射積分方程式の導出




Qrnlcyjsjflesm




1次関数を学習するには 学林舎ニュース 教材出版 学林舎 学習教材の制作 販売 理科実験工作教材 アメリカの教科書



1




範囲に制限がない時 なんでsinとcosのときは 2npなのにtanのときは npな Clear




数学 B 三角関数を解とする3次方程式 愛媛大 一橋大 大学入試数学の考え方と解法




微分方程式の解き方を分かりやすく解説



48s96ub7b0z5f Net Shisuukansuu Chikan



三角比 三角関数が苦手な人にお勧め 方程式も不等式も速効 秘伝 たんタンくるクル を公開しよう 金色の湯たんぽ



0 件のコメント:
コメントを投稿